本文共 6940 字,大约阅读时间需要 23 分钟。
Netty 入门
疯狂创客圈 Java 分布式聊天室【 亿级流量】实战系列之 -入门【 】
文章目录
前言:
问题: 我们需要高度优化的协议
现在我们使用通用应用程序或包进行通信。例如,我们经常使用HTTP客户端库从Web服务器检索信息,并通过Web服务调用远程过程调用。然而,通用协议或其实现有时不能很好地扩展。这就像我们不使用通用HTTP服务器来交换大量文件,电子邮件和近实时消息,如财务信息和多人游戏数据。
我们需要的是高度优化的协议实现,专门用于特殊目的。例如,您可能希望实现针对基于AJAX的聊天应用程序,媒体流或大型文件传输进行了优化的HTTP服务器。你甚至可以设计和实施一个全新的协议,这个协议是根据你的需要而定制的。另一个不可避免的情况是当您必须处理旧版专有协议以确保与旧系统的互操作性。在这种情况下重要的是我们能够快速实现该协议,而不会牺牲最终应用程序的稳定性和性能。
方案
Netty项目是为了快速开发可维护的高性能高可扩展性协议服务器和客户端而努力提供异步事件驱动的网络应用程序框架和工具。换句话说,Netty是一个NIO客户端服务器框架,可以快速轻松地开发诸如协议服务器和客户端之类的网络应用程序。它大大简化了网络编程流程,如TCP和UDP套接字服务器开发。
“快速和容易”并不意味着由此产生的应用程序将遭受可维护性或性能问题的困扰。Netty经过精心设计,实现了许多协议,如FTP,SMTP,HTTP以及各种基于二进制和基于文本的传统协议。因此,Netty成功地找到了一种方法来实现轻松的开发,性能,稳定性和灵活性,而无需妥协。
有些用户可能已经找到了声称具有相同优势的其他网络应用程序框架,您可能想问问Netty与他们的区别。答案是它建立的哲学。Netty旨在为您提供API和执行方面最舒适的体验,从第一天开始。这不是有形的东西,但你会意识到,这个哲学将使你的生活更容易,当你阅读本指南和玩Netty的时候。
好了,以上就是关于netty的一个官网的初步介绍。
下面进入搭建最简单的服务器的环节,我这里会按照官网的思路走,不过不会完全一点不差。
好了,我们开始。
建立项目
首先我们需要建立项目,如下图所示:
项目名称是NettyDemo,官网建议使用JDK1.6以上,我这里使用的JDK1.8,然后加入使用maven导入Netty依赖:
io.netty netty-all 4.1.6.Final
那么现在我们可以正式开始我们的项目编写了。
编写一个Discard Handler 处理器
编写一个Discard服务器(按我理解就是啥也不干的服务器,别着急反驳,往下看)
世界上最简单的协议不是“hello world”,而是。。。。什么也不做的协议Discard,丢弃的意思,服务端丢弃,那就是啥也不做的协议呗(尝试把协议理解为用户自定义功能)。
想要实现一个Discard协议,那么我们唯一需要做的就是忽略所有接收到的数据。让我们从处理器实现开始,它处理由netty生成的I/O事件。 首先我们创建一个java包:netty_beginner,然后在里面创建一个类DiscardServerHandler 类的内容如下:package netty_beginner;import io.netty.buffer.ByteBuf;import io.netty.channel.ChannelHandlerContext;import io.netty.channel.ChannelInboundHandlerAdapter;/**- Created by moon on 2017/4/5. */ public class DiscardServerHandler extends ChannelInboundHandlerAdapter { // (1) @Override public void channelRead(ChannelHandlerContext ctx, Object msg) throws Exception { // (2) // super.channelRead(ctx, msg); ((ByteBuf) msg).release(); // (3) ByteBuf in = (ByteBuf) msg; try { while (in.isReadable()) { System.out.print((char) in.readByte()); System.out.flush(); } } finally { ReferenceCountUtil.release(msg); } } @Override public void exceptionCaught(ChannelHandlerContext ctx, Throwable cause) throws Exception { // (5) // super.exceptionCaught(ctx, cause); cause.printStackTrace(); ctx.close(); } } DiscardServerHandler 继承自ChannelInboundHandlerAdapter,它是 ChannelInboundHandler的实现。提供可以覆盖的各种事件处理程序方法。现在,只需要扩展ChannelInboundHandlerAdapter即可,而不是自己实现处理程序接口。
在这里,我们重写通道读取channelRead()事件处理方法。每当从客户端收到新数据时,都会使用接收到的消息调用此方法。 在这个例子中,接收到的消息的类型是ByteBuf。
为了实现DISCARD 丢弃的功能,处理程序必须丢弃掉收到的消息。
ByteBuf是一个引用计数对象,必须通过release()方法显式释放。请记住,处理程序有责任释放传递给处理程序的引用计数对象。通常,channelRead()处理方法的实现方式如下:
@Overridepublic void channelRead(ChannelHandlerContext ctx, Object msg) { try { // Do something with msg } finally { ReferenceCountUtil.release(msg); }} 当由于I / O错误或由于在处理事件时抛出异常而使得Netty抛出异常时,exceptionCaught() 事件将会被Throwable抛出。
在大多数情况下,应该记录捕获到的异常,并在此关闭其关联的通道,虽然这种方法的实现可以根据你想要处理的异常情况而有所不同。例如,您可能希望在关闭连接之前发送带有错误代码的响应消息。
编写一个Discard 服务器
到目前位置一切顺利。我们已经实现了DISCARD服务器的前半部分。现在剩下的是写入使用DiscardServerHandler启动服务器的main()方法。
我们创建另外一个类:DiscardServer,实现 Discard 服务的功能。
如下:
package netty_beginner;import io.netty.bootstrap.ServerBootstrap;import io.netty.channel.ChannelFuture;import io.netty.channel.ChannelInitializer;import io.netty.channel.ChannelOption;import io.netty.channel.EventLoopGroup;import io.netty.channel.nio.NioEventLoopGroup;import io.netty.channel.socket.SocketChannel;import io.netty.channel.socket.nio.NioServerSocketChannel;/**- Created by moon on 2017/4/5. */ public class DiscardServer { private int port; public DiscardServer(int port) { this.port = port; } public void run() throws InterruptedException { EventLoopGroup bossGroup = new NioEventLoopGroup(); // (1) EventLoopGroup workerGroup = new NioEventLoopGroup(); try { ServerBootstrap b = new ServerBootstrap(); // (2) b.group(bossGroup, workerGroup) .channel(NioServerSocketChannel.class) // (3) .childHandler(new ChannelInitializer () { // (4) @Override public void initChannel(SocketChannel ch) throws Exception { ch.pipeline().addLast(new DiscardServerHandler()); } }) .option(ChannelOption.SO_BACKLOG, 128) // (5) .childOption(ChannelOption.SO_KEEPALIVE, true); // (6) // Bind and start to accept incoming connections. ChannelFuture f = b.bind(port).sync(); // (7) // Wait until the server socket is closed. // In this example, this does not happen, but you can do that to gracefully // shut down your server. f.channel().closeFuture().sync(); } finally { workerGroup.shutdownGracefully(); bossGroup.shutdownGracefully(); } } public static void main(String[] args) throws InterruptedException { int port; if (args.length > 0) { port = Integer.parseInt(args[0]); } else { port = 8080; } new DiscardServer(port).run(); } } 线程组
NioEventLoopGroup 是一个处理I / O操作的多线程事件循环线程组。
Netty为不同类型的传输提供了各种EventLoopGroup实现。在这个例子中,使用两个NioEventLoopGroup线程组。一般的服务器,都使用两个以上的线程组。
-
第一个,通常称为“Boss”,用于接受客户端的连接。
-
第二个,通常称为“Worker”,一旦“Boss” 接受客户端的连接,并将接受的连接注册给“Worker”。
“Boss”负责连接的监听,“Worker”负责处理连接的输入和输出。
一个线程组,包含一条或者多条线程。
启动帮助类
ServerBootstrap是一个帮助类,用于设置服务器。可以不用ServerBootstrap直帮助类,直接使用Channel设置服务器。但是,这是一个繁琐的过程,在大多数情况下您不需要这样做。
在这里,我们指定使用NioServerSocketChannel类来实例化一个新的Channel来接受传入的连接。(可以这么理解,每个客户端连接我们服务端,我们都会为他们创建一个channel,那么这个channel对于面向对象的我们来说就是一个类,我们同意对于我们接受到的连接都初始化为:NioServerSocketChannel。
这里指定的处理程序将始终由新接受的Channel进行评估。ChannelInitializer是一个特殊的处理程序,旨在帮助用户配置新的Channel。很可能您想通过添加一些处理程序(如DiscardServerHandler)来配置新Channel的ChannelPipeline来实现您的网络应用程序。随着应用程序的复杂化,您可能会在管道中添加更多的处理程序,并将这个匿名类最终提取到顶级类中。(个人感觉说白了就是想自己实现包含自己处理逻辑的Channel,但是又需要包含一些通用的原有功能,咋办,继承呗,这就是为什么上面的DiscardServerHandler继承netty的类) 您还可以设置特定于Channel实现的参数。我们正在编写一个TCP / IP服务器,因此我们可以设置套接字选项,如tcpNoDelay和keepAlive。请参阅ChannelOption的apidocs和特定的ChannelConfig实现,以获得有关支持的ChannelOptions的概述。
设置Channel 通道的选项
你有没有注意到option()和childOption()?
option()用于配置 服务器连接监听通道 ,也就是 NioServerSocketChannel。
childOption()用于配置每一个客户端连接成功的通道 —— NioSocketChannel。
我们现在准备好了。剩下的是绑定到端口并启动服务器。这里,我们绑定机器中端口 (比如 8080)。如果有多个地址,您现在可以根据需要调用 bind()方法多次(具有不同的绑定地址)。
恭喜,到了现在这个阶段我们已经完成了。下面可以进行尝试,那么在尝试之前,我要说一句,这个例子非常好,就是一点比较费解,即使我开始测试。
步骤是:
- 首先启动服务器的main方法。
- 然后,通过telnet ,本机8080端口发送内容,看看是否成功
测试:发送消息到Discard服务器
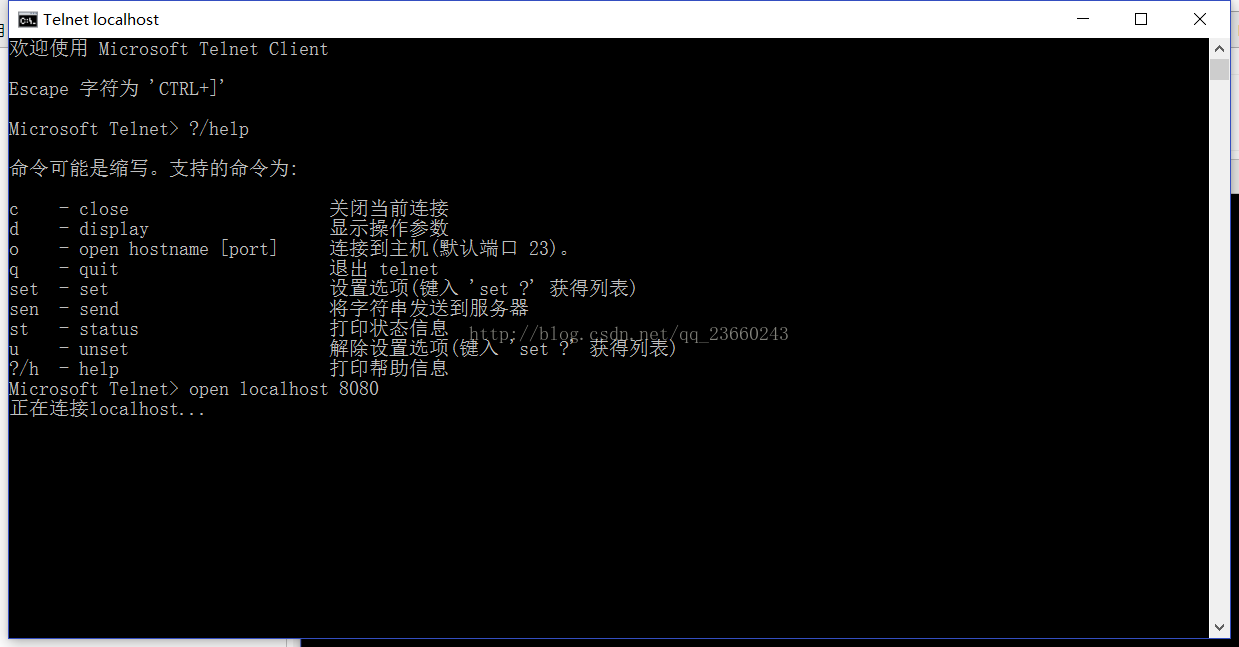
我们打开cmd,输入 telnet,进入一个新的窗口:
我们使用 telnet 命令:open localhost 8080 ,开启Discard服务器的telnet连接。
如下图:
如果忘记了命令,可以使用帮助命令。 这个帮助命令为: ?/help
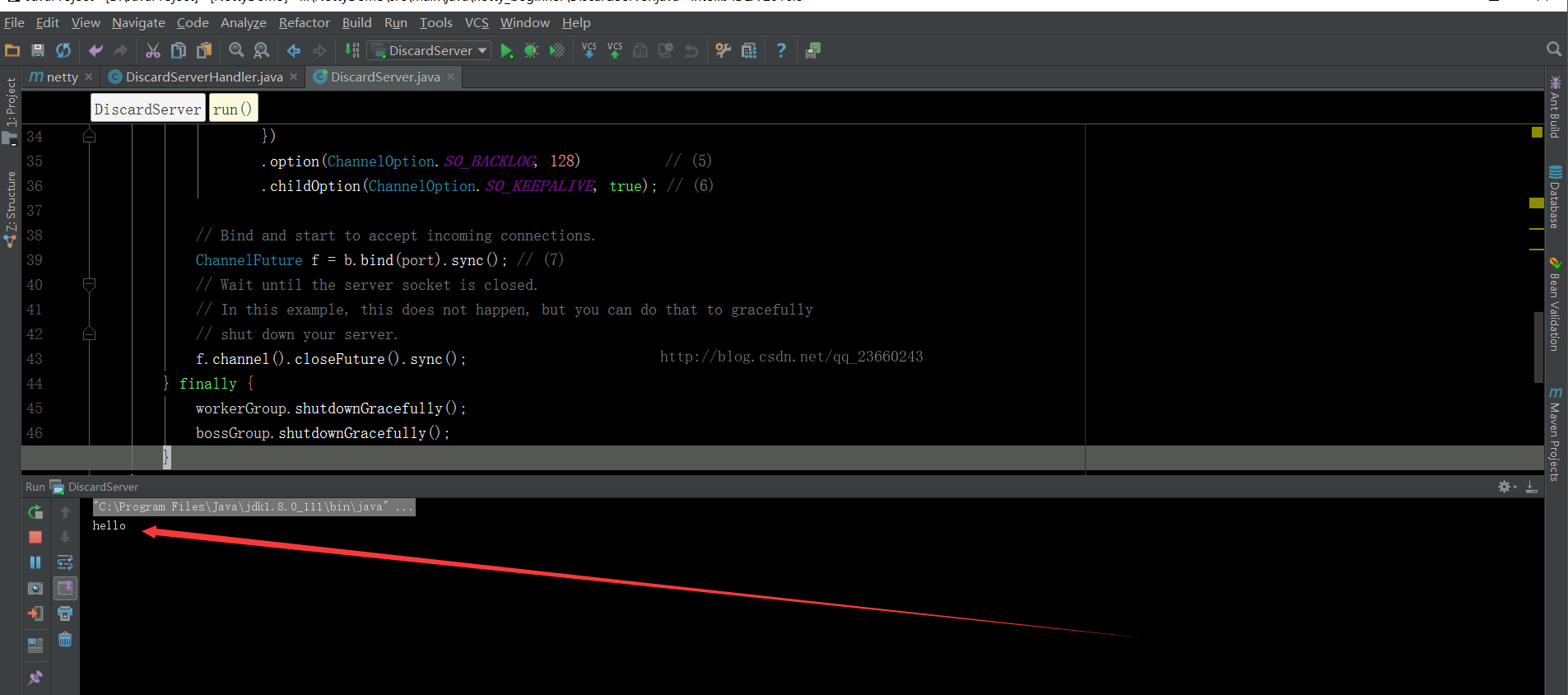
连接成功后,我们可以输入任何内容,比如 hello,在idea控制台会挨个字符输出:
写在最后
至此为止,可以看到,Netty 的开发,其实是容易入门滴。
下一篇: Netty 的 Echo 服务器,比这个例子稍微复杂一点点。
疯狂创客圈 Java 死磕系列
- Java (Netty) 聊天程序【 亿级流量】实战 开源项目实战
- Netty 源码、原理、JAVA NIO 原理
- Java 面试题 一网打尽
- 疯狂创客圈